Searching algorithm details

Searching algorithm details are given below:

What is Searching Algorithm?

In Searching algorithm details ,Searching algorithm is a algorithm for searching or retrieving an element from an data structure, where elements stored.

TYPES OF SERACHING ALGORITHM BASED ON SEARCH OPERATION

There are two types of search algorithm based on serach operation.

Sequential Search: In this, the list or array is traversed sequentially and every element is checked. For example: Linear Search

Linear Search:Linear Search is defined as a sequential search algorithm that starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set.

How Linear Search Works?

• Step 1: First, read the search element (Target element) in the array.
• Step 2: Set an integer i = 0 and repeat steps 3 to 4 till i reaches the end of the array.
• Step 3: Match the key with arr[i].
• Step 4: If the key matches, return the index. Otherwise, increment i by 1.

Searching Algorithm Details

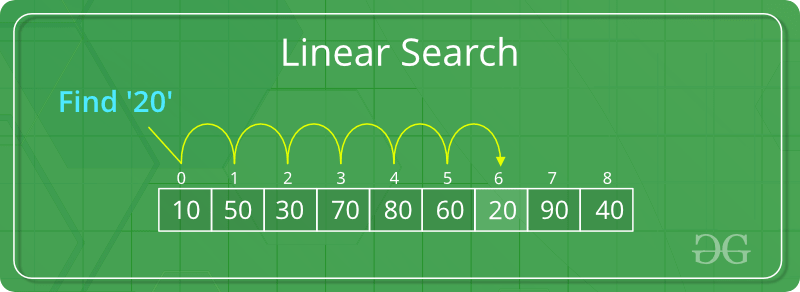
Illustration of Linear Search:

Consider the array arr[] = {10, 50, 30, 70, 80, 20, 90, 40} and key = 20

 

Step 1: Set i = 0 and check key with arr[0].

 

Searching Algorithm Details

Compare key with index 0

Step 2: key and arr[0] are not the same. So make i = 1 and match key with arr[1].

Searching Algorithm Details

 

 

Step 3: arr[1] and key are different. Increment i and compare key with arr[2].

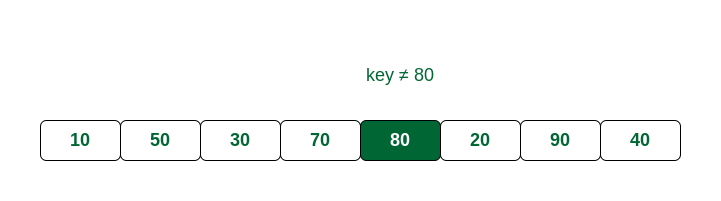
Compare key with index 2

Step 4: arr[2] is not the same with key. Increment i and compare key with arr[3].

Searching Algorithm Details

 

Compare key with index 3

Step 5: key and arr[3] are different. Make i = 4 and compare key with arr[4].

Compare key with index 4

Step 6: key and arr[4] are not same. Make i = 5 and match key with arr[5].

We can see here that key is present at index 5.

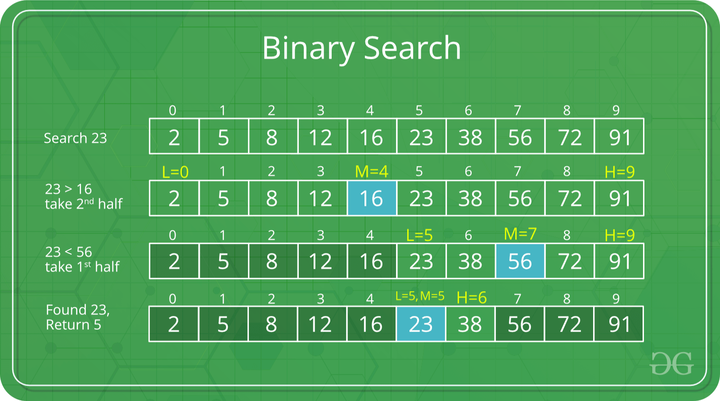
Interval Search: These algorithms are specifically designed for searching in sorted data-structures. These type of searching algorithms are much more efficient than Linear Search as they repeatedly target the center of the search structure and divide the search space in half. For Example: Binary Search.

Binary Search to find the element “23” in a given list of numbers

 

 

Searching Algorithm Details

 

OTHER SEARCHING ALGORITHMS

• Exponential search /Doubling/galloping search

Exponential search is also known as doubling or galloping search. This mechanism is used to find the range where the search key may present. If L and U are the upper and lower bound of the list, then L and U both are the power of 2. For the last section, the U is the last position of the list. For that reason, it is known as exponential.

After finding the specific range, it uses the binary search technique to find the exact location of the search key.

The complexity of Exponential Search Technique

• Time Complexity: O(1) for the best case. O(log2 i) for average or worst case. Where i is the location where search key is present.
• Space Complexity: O(1)

Input and Output

Input:
A sorted list of data:
10 13 15 26 28 50 56 88 94 127 159 356 480 567 689 699 780 850 956 995
The search key 780
Output:
Item found at location: 16

Algorithm
binarySearch(array, start, end, key)
Input: An sorted array, start and end location, and the search key
Output − location of the key (if found), otherwise wrong location.
Begin
   if start <= end then
      mid := start + (end - start) /2
      if array[mid] = key then
         return mid location
      if array[mid] > key then
         call binarySearch(array, mid+1, end, key)
      else when array[mid] < key then
         call binarySearch(array, start, mid-1, key)
   else
      return invalid location
End
exponentialSearch(array, start, end, key)
Input: An sorted array, start and end location, and the search key
Output: location of the key (if found), otherwise wrong location.
Begin
   if (end – start) <= 0 then
      return invalid location
   i := 1
   while i < (end - start) do
      if array[i] < key then
         i := i * 2 //increase i as power of 2
      else
         terminate the loop
   done
JAVASCRIPT PROGRAM FOR EXPONENTIAL SEARCH

The exponential search come right first:
1function exponentialSearch(arrayToSearch, valueToSearch, length) {
2  if (arrayToSearch[0] == valueToSearch) {
3    return 0;
4  }
5
6  var i = 1;
7  while (i < length && arrayToSearch[i] <= valueToSearch) {
8    i = i * 2;
9  }
10  return binarySearch(
11    arrayToSearch,
12    valueToSearch,
13    i / 2,
14    Math.min(i, length - 1)
15  );
16}


1function binarySearch(arrayToSearch, valueToSearch, start, end) {
2  if (start <= end) {
3    var middle = Math.ceil((end + start) / 2);
4    var middleValue = arrayToSearch[middle];
5    if (middleValue === valueToSearch) {
6      return middle;
7    } else if (valueToSearch < middleValue) {
8      end = middle - 1;
9    } else {
10      start = middle + 1;
11    }
12    return binarySearch(arrayToSearch, valueToSearch, start, end);
13  }
14  return -1;
15}