Backtracking Algorithm Description
Backtracking Algorithm description is given below:
Backtracking Algorithm can be said as a improvement of Brute Force algorithm.
Backtracking as a general algorithmic technique that considers searching every possible combination in order to solve a computational problems
Types of Problem in backtracking – Three
- Decision Problem – Here, we search for a feasible solution.
- Optimization Problem – Here, we search for the best solution.
- Enumeration Problem – Here, we find all feasible solutions.
It finds a solution by building a solution step by step,using recursive calling.
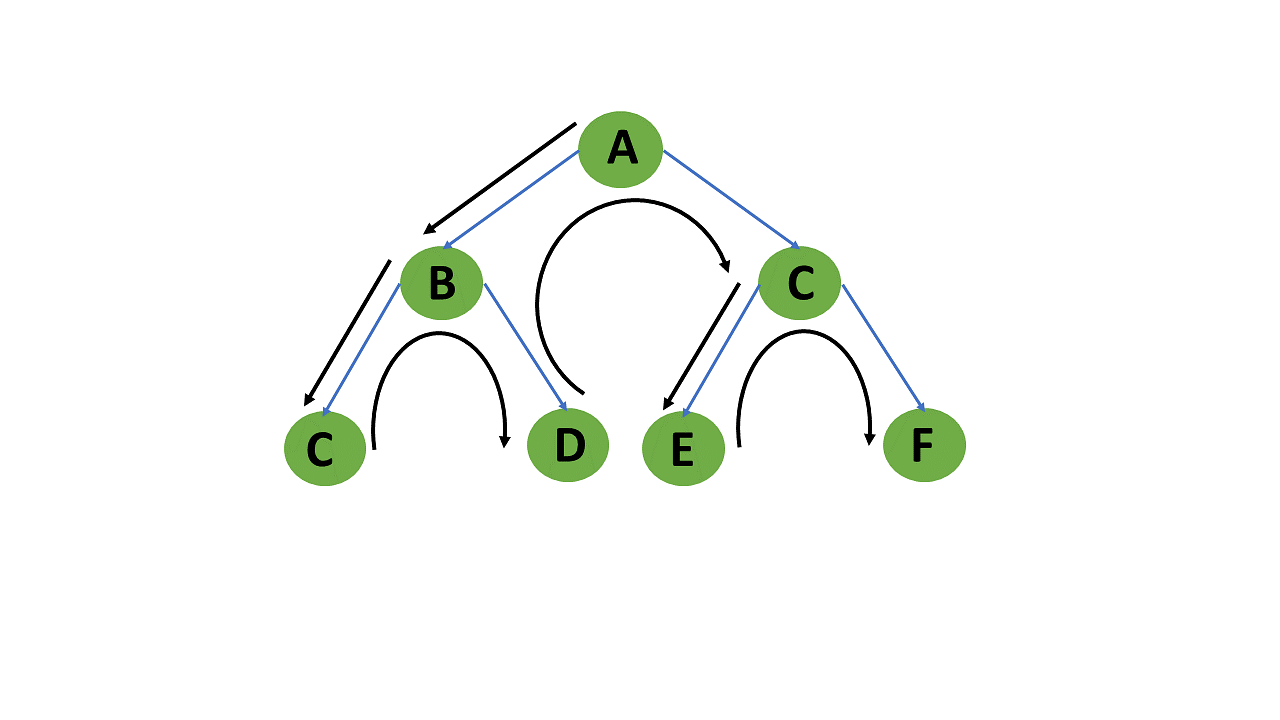
A search tree known as the state-space tree is used to find these solutions
Each branch in a state-space tree represents a variable, and each level represents a solution.
Which method of Backtracking algorithm used for searching solutions?
A backtracking algorithm uses the depth-first search method.
Backtracking Algorithm description is given below:
Backtracking Algorithm can be said as a improvement of Brute Force algorithm.
Backtracking as a general algorithmic technique that considers searching every possible combination in order to solve a computational problems
Types of Problem in backtracking – Three
- Decision Problem – Here, we search for a feasible solution.
- Optimization Problem – Here, we search for the best solution.
- Enumeration Problem – Here, we find all feasible solutions.
It finds a solution by building a solution step by step,using recursive calling.
A search tree known as the state-space tree is used to find these solutions
Each branch in a state-space tree represents a variable, and each level represents a solution.
Which method of Backtracking algorithm used for searching solutions?
A backtracking algorithm uses the depth-first search method.
What is a Depth-First Search Algorithm?
The depth-first search or DFS algorithm traverses or explores data structures, such as trees and graphs. The algorithm starts at the root node (in the case of a graph, you can use any random node as the root node) and examines each branch as far as possible before backtracking.
Backtracking algorithm description
When a dead-end occurs in any iteration, the Depth First Search (DFS) method traverses a network in a deathward motion and uses a stack data structure t o remember to acquire the next vertex to start a search.
The depth-first search or DFS algorithm traverses or explores data structures, such as trees and graphs. The algorithm starts at the root node (in the case of a graph, you can use any random node as the root node) and examines each branch as far as possible before backtracking.
 |
| Backtracking algorithm description |
When a dead-end occurs in any iteration, the Depth First Search (DFS) method traverses a network in a deathward motion and uses a stack data structure t o remember to acquire the next vertex to start a search.
Example of Depth-First Search Algorithm
The outcome of a DFS traversal of a graph is a spanning tree. A spanning tree is a graph that is devoid of loops. To implement DFS traversal, you need to utilize a stack data structure with a maximum size equal to the total number of vertices in the graph.
To implement DFS traversal, you need to take the following stages.
Step 1: Create a stack with the total number of vertices in the graph as the size.
Step 2: Choose any vertex as the traversal's beginning point. Push a visit to that vertex and add it to the stack.
Step 3 - Push any non-visited adjacent vertices of a vertex at the top of the stack to the top of the stack.
Step 4 - Repeat steps 3 and 4 until there are no more vertices to visit from the vertex at the top of the stack.
Step 5 - If there are no new vertices to visit, go back and pop one from the stack using backtracking.
Step 6 - Continue using steps 3, 4, and 5 until the stack is empty.
Step 7 - When the stack is entirely unoccupied, create the final spanning tree by deleting the graph's unused edges.
Consider the following graph as an example of how to use the dfs algorithm.
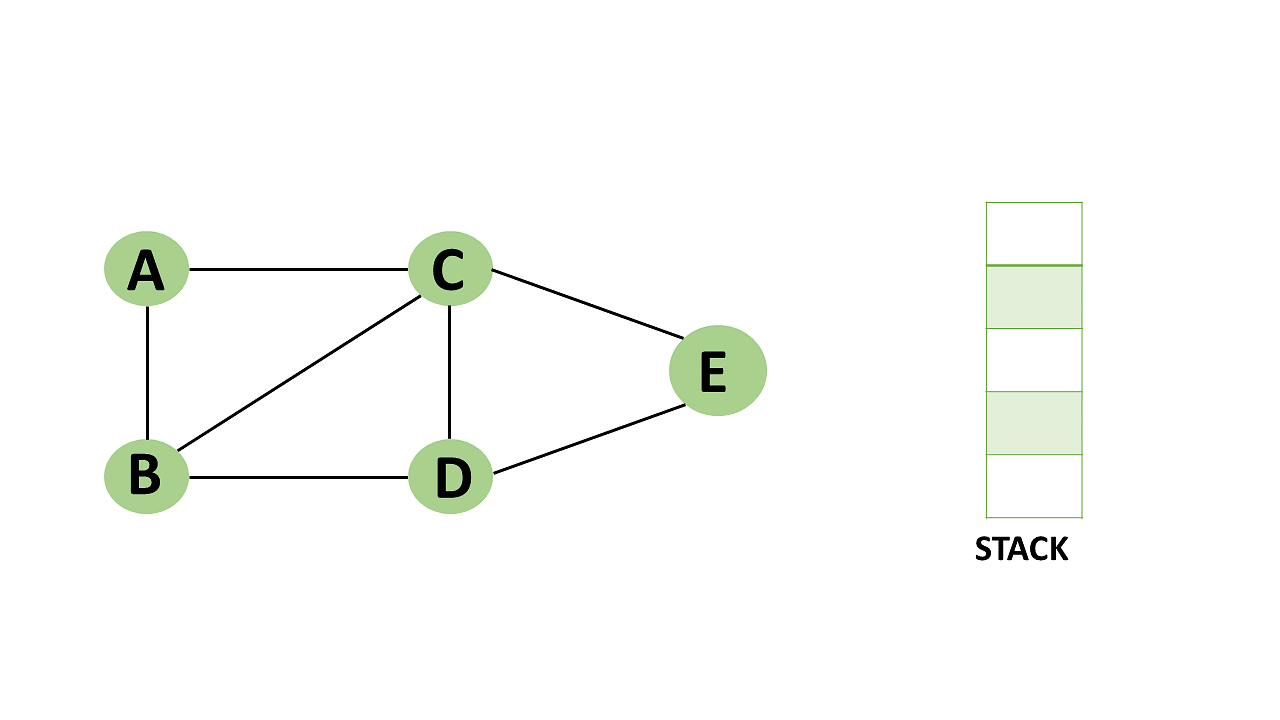
Backtracking algorithm description
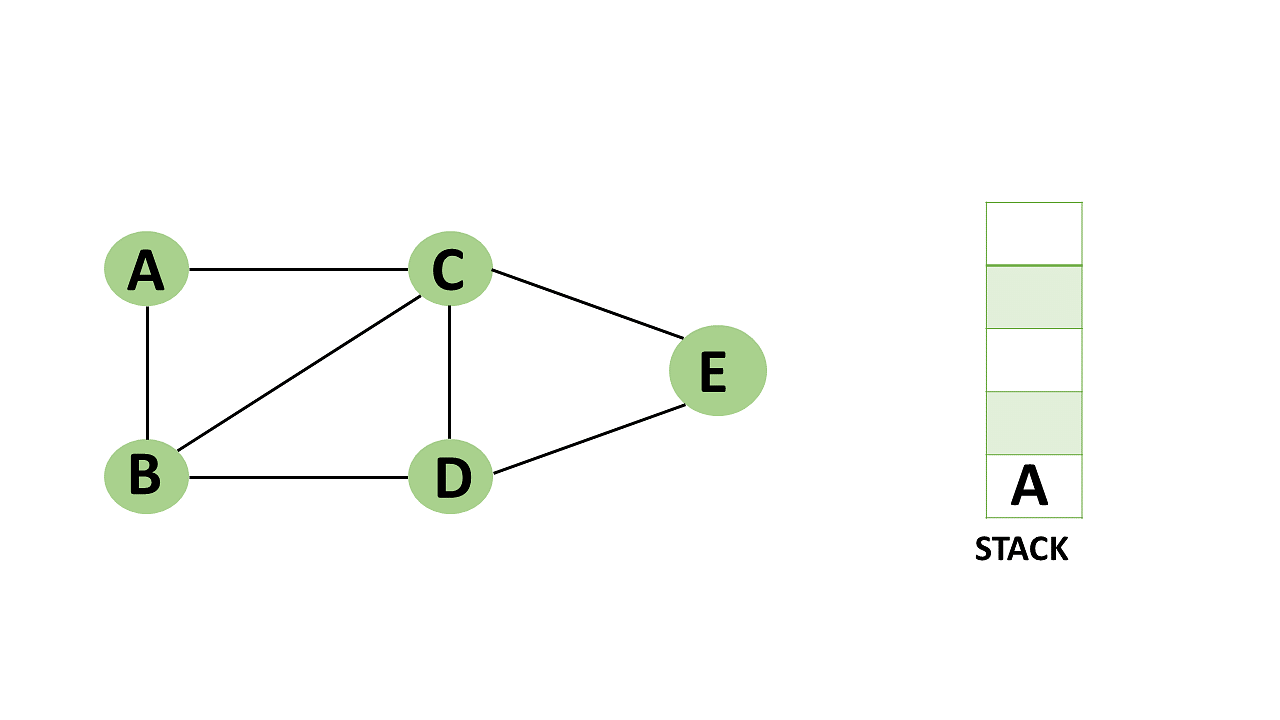
Step 1: Mark vertex A as a visited source node by selecting it as a source node.
- You should push vertex A to the top of the stack.
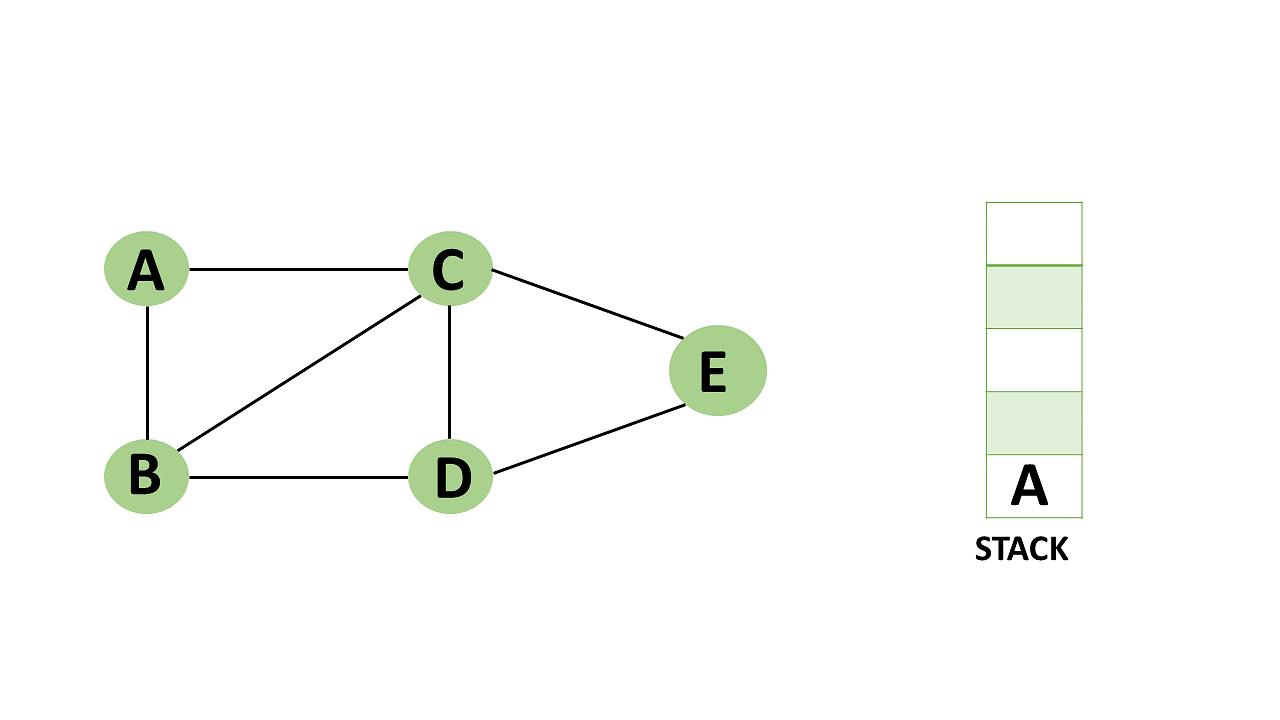
Backtracking algorithm description
Step 2: Any nearby unvisited vertex of vertex A, say B, should be visited.
- You should push vertex B to the top of the stack.
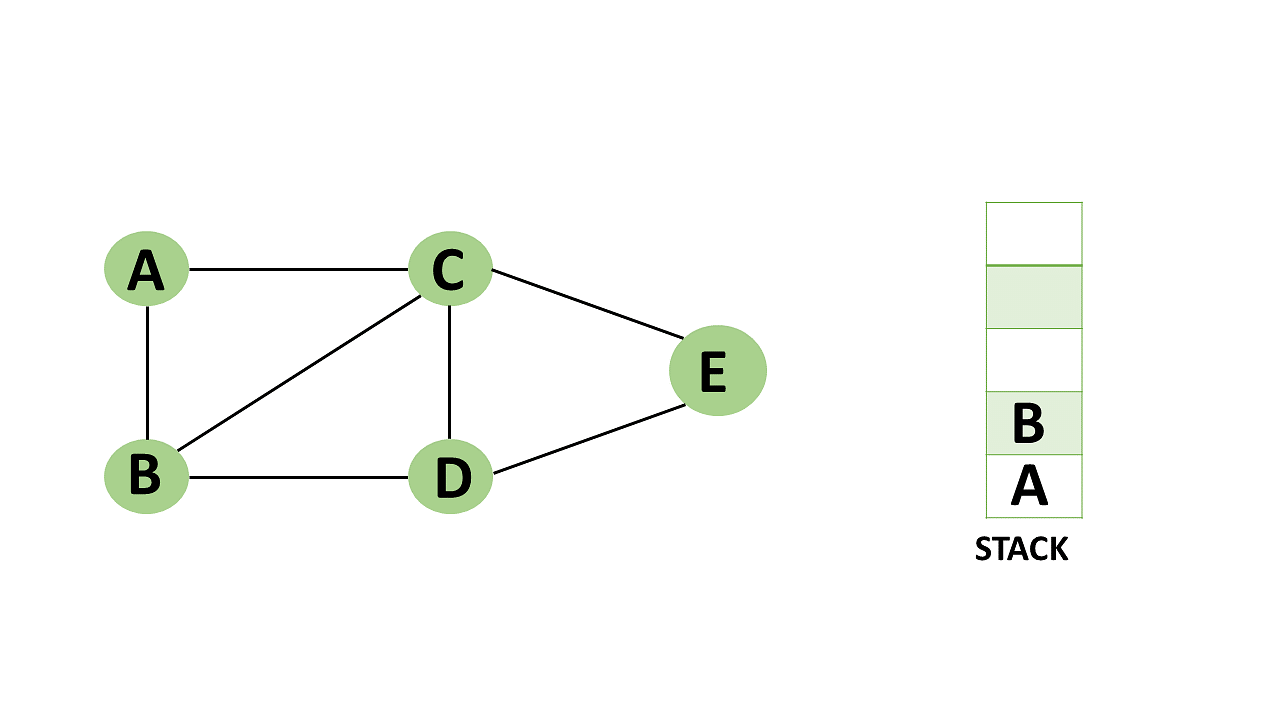
Backtracking algorithm description
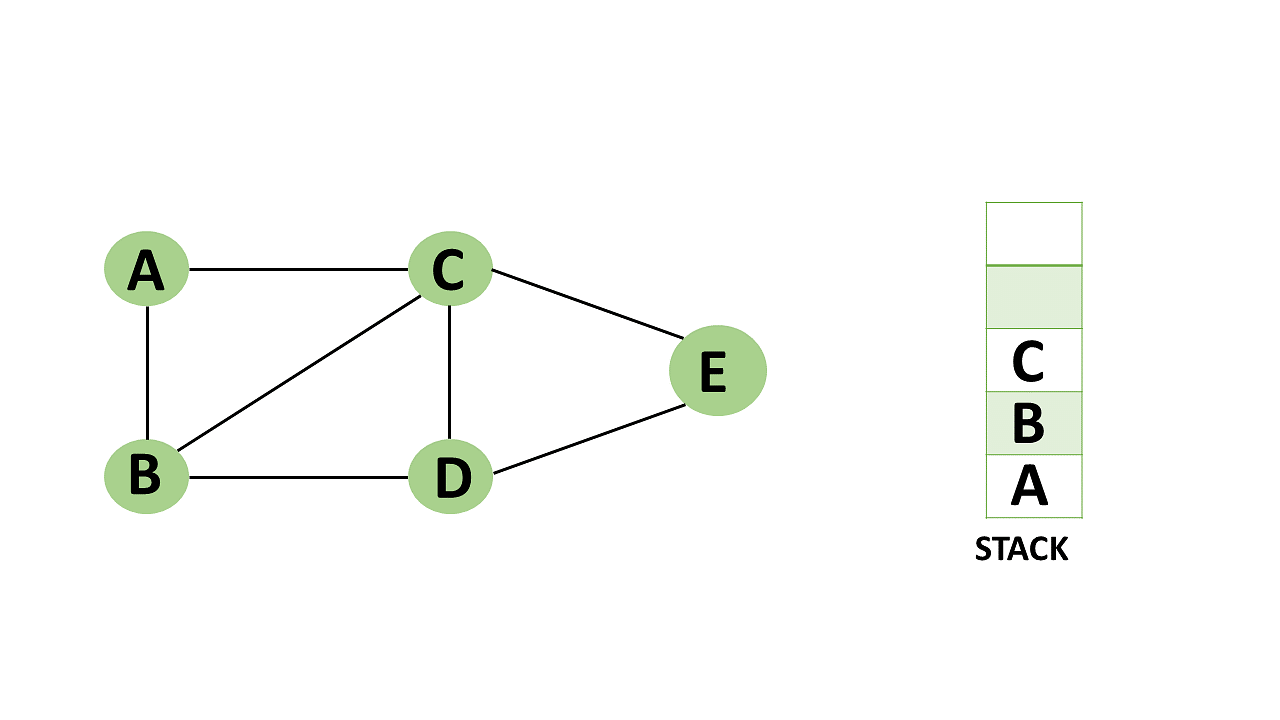
Step 3: From vertex C and D, visit any adjacent unvisited vertices of vertex B. Imagine you have chosen vertex C, and you want to make C a visited vertex.
- Vertex C is pushed to the top of the stack.
Backtracking algorithm description
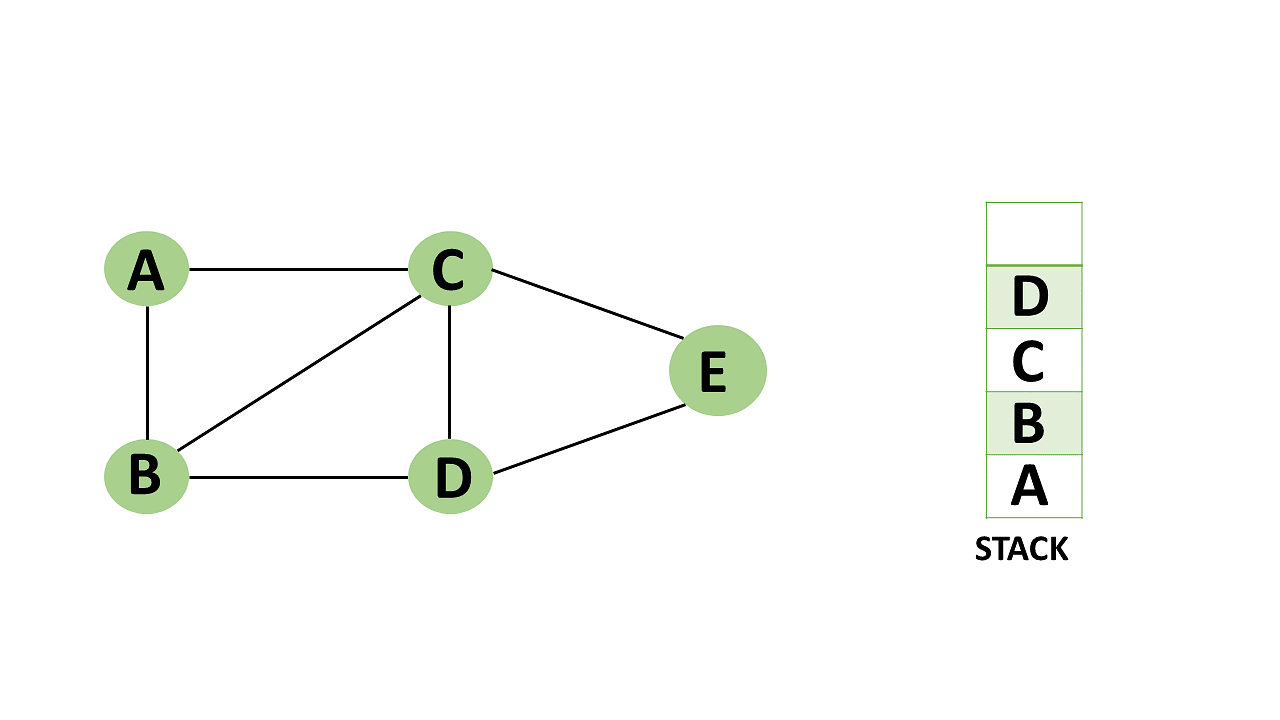
Step 4: You can visit any nearby unvisited vertices of vertex C, you need to select vertex D and designate it as a visited vertex.
- Vertex D is pushed to the top of the stack.
Backtracking algorithm description
Backtracking algorithm description
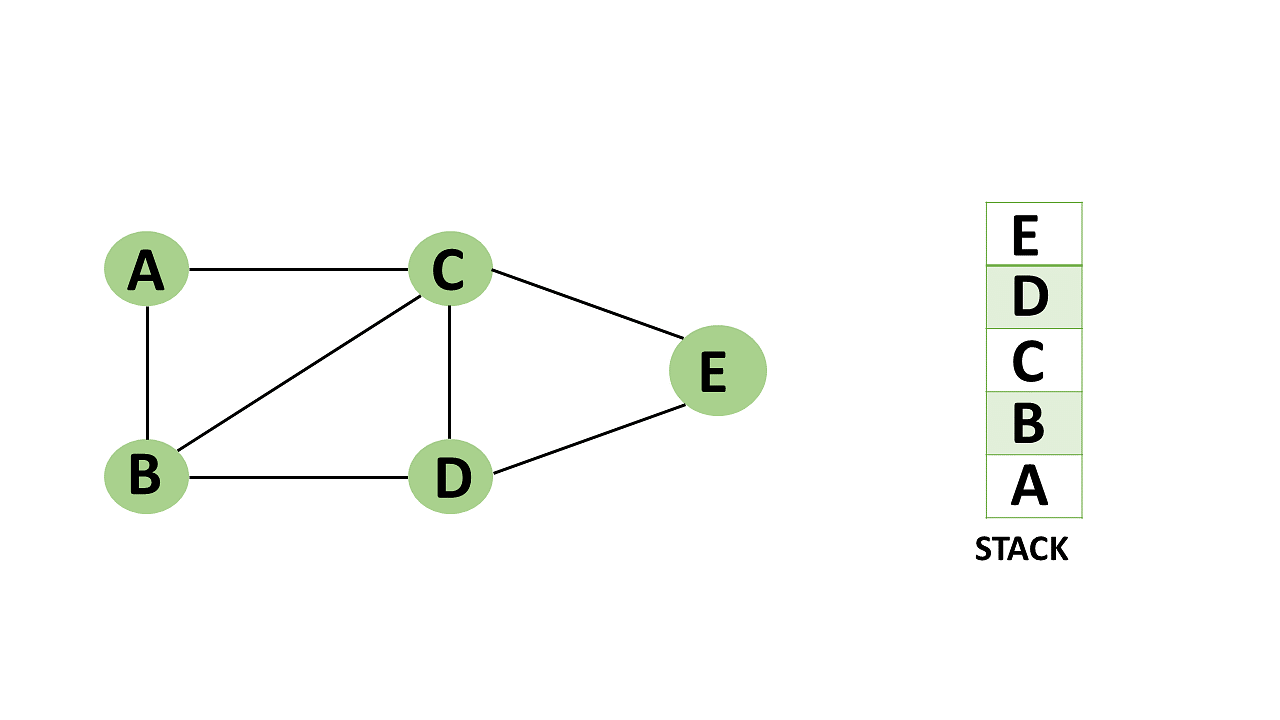
Step 5: Vertex E is the lone unvisited adjacent vertex of vertex D, thus marking it as visited.
- Vertex E should be pushed to the top of the stack.
Backtracking algorithm description
Step 6: Vertex E's nearby vertices, namely vertex C and D have been visited, pop vertex E from the stack.
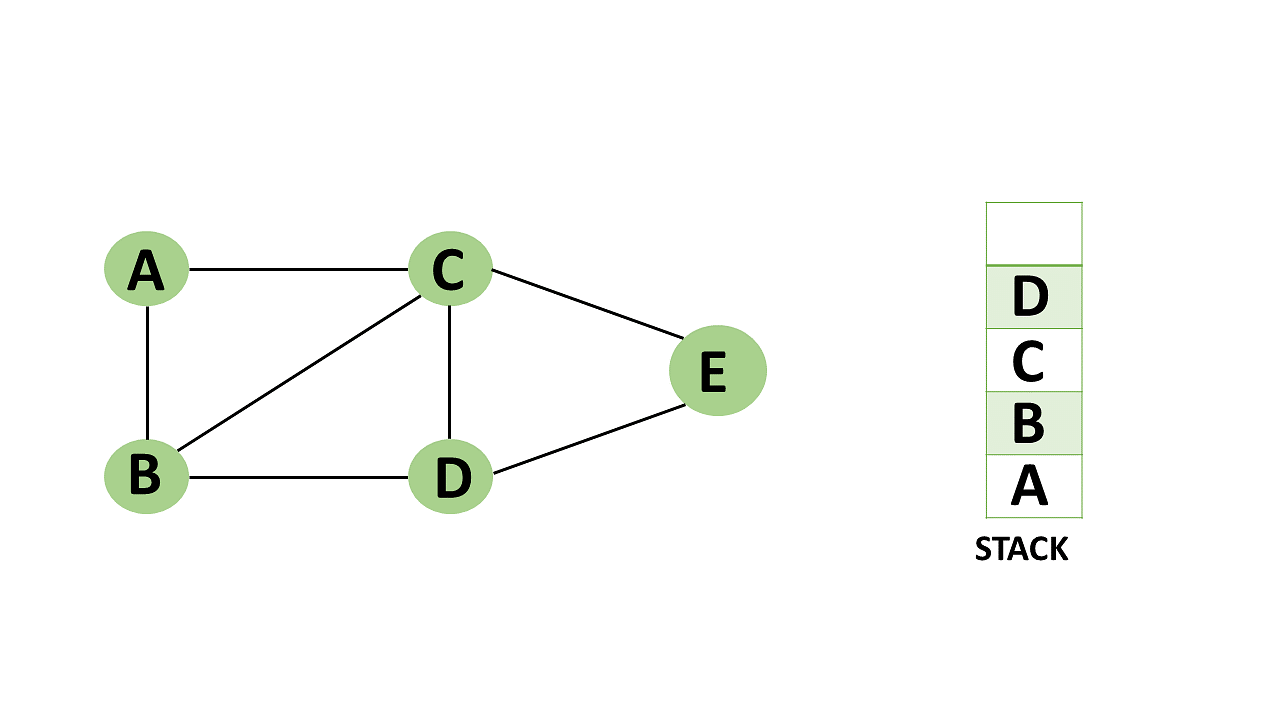
Backtracking algorithm description
Step 7: Now that all of vertex D's nearby vertices, namely vertex B and C, have been visited, pop vertex D from the stack.
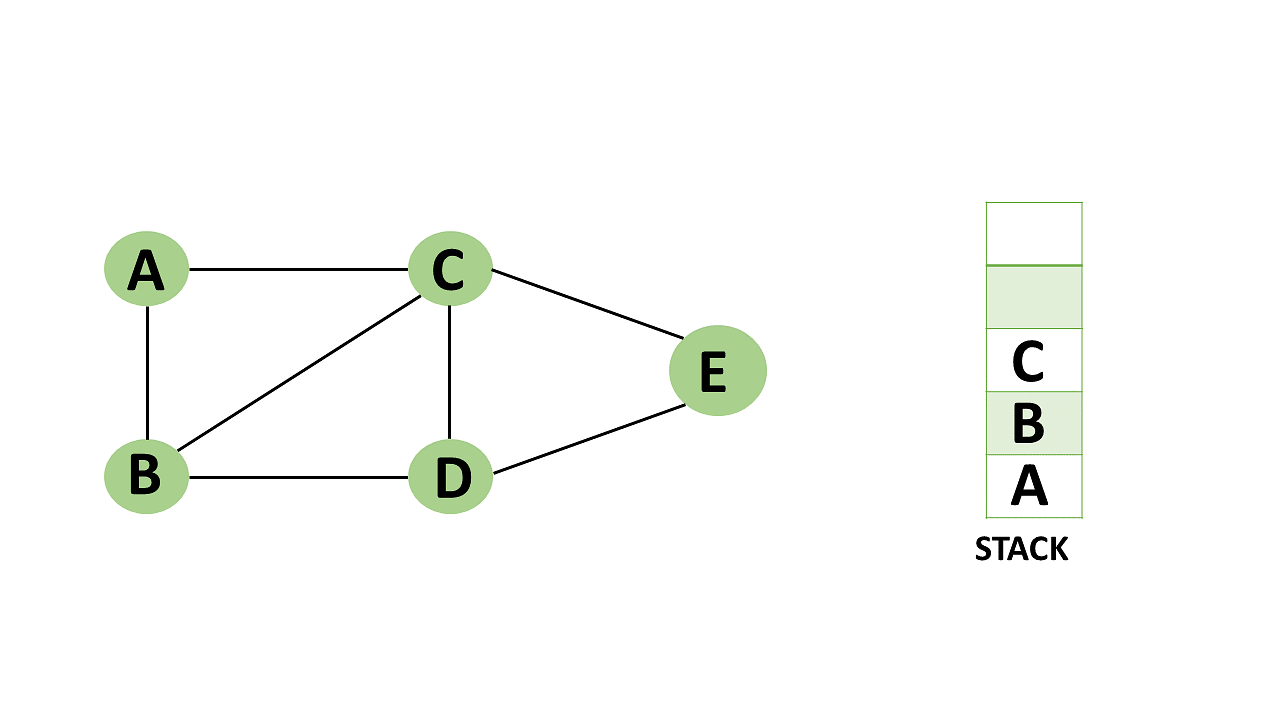
Backtracking algorithm description
Step 8: Similarly, vertex C's adjacent vertices have already been visited; therefore, pop it from the stack.
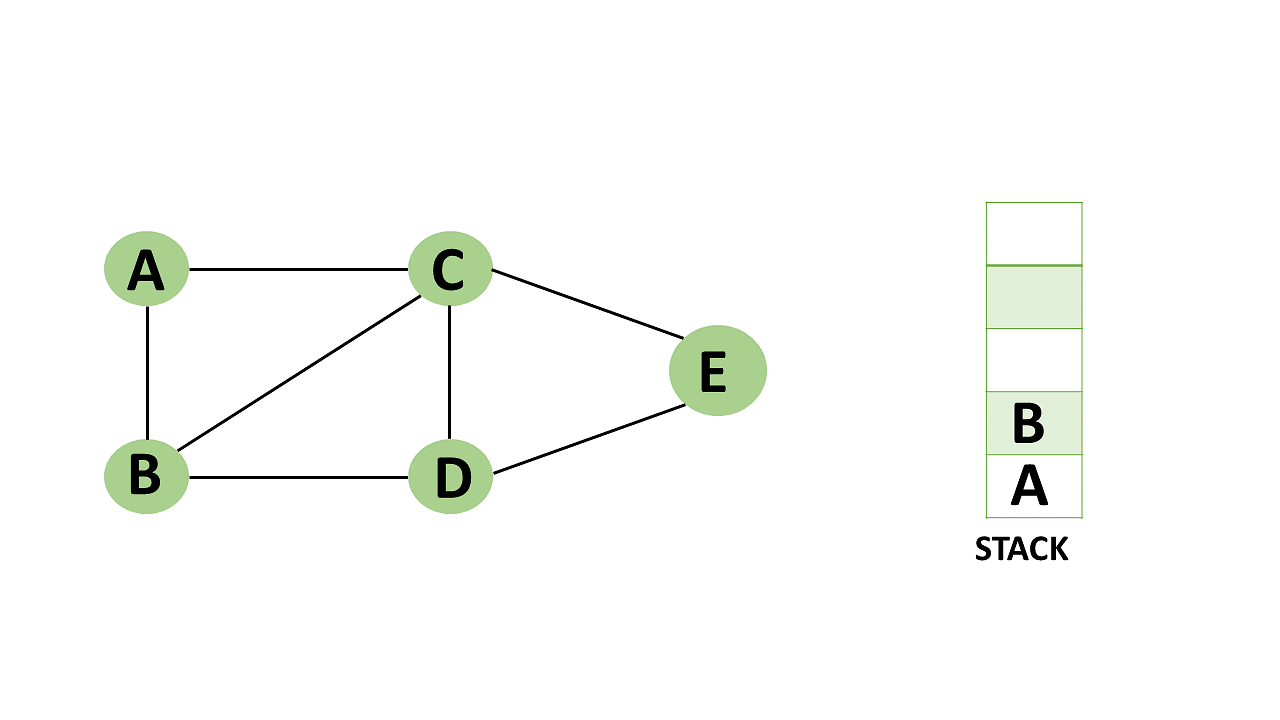
Backtracking algorithm description
Step 9: There is no more unvisited adjacent vertex of b, thus pop it from the stack.

Backtracking algorithm description
Step 10: All of the nearby vertices of Vertex A, B, and C, have already been visited, so pop vertex A from the stack as well.
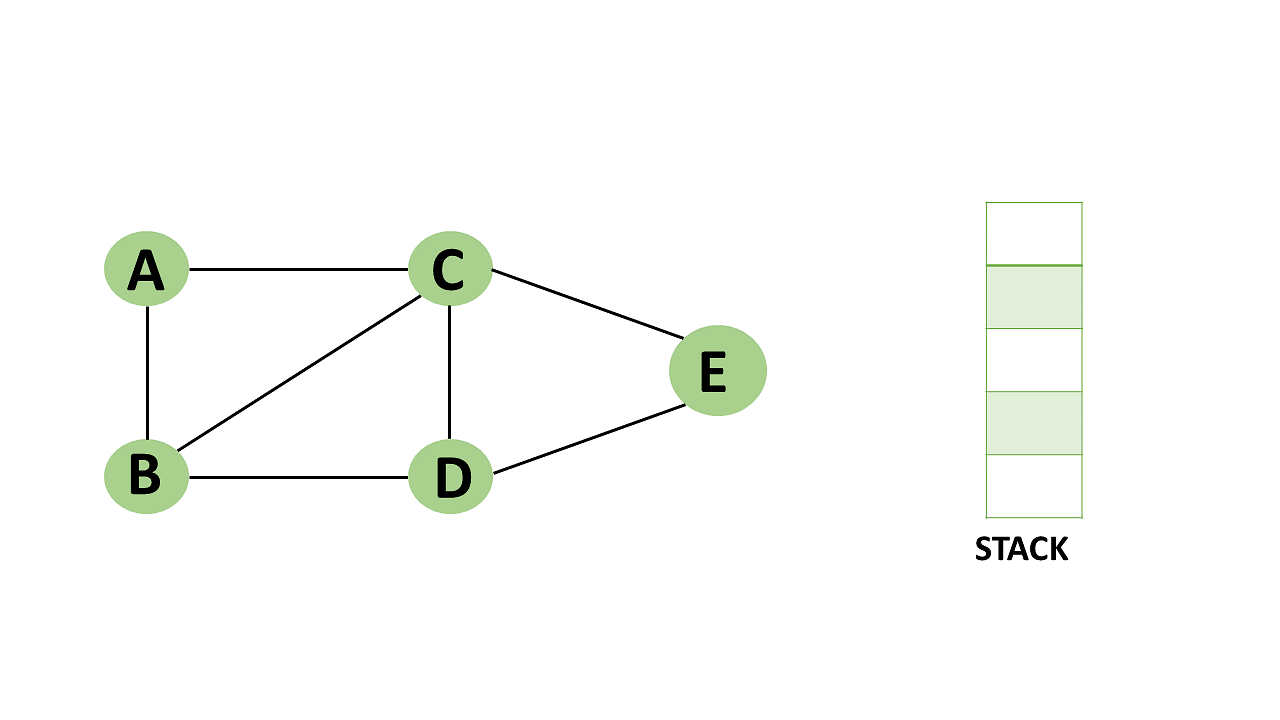
Backtracking algorithm description
When a dead-end occurs in any iteration, the Depth First Search (DFS) method traverses a network in a deathward motion and uses a stack data structure to remember to acquire the next vertex to start a search.
The outcome of a DFS traversal of a graph is a spanning tree. A spanning tree is a graph that is devoid of loops. To implement DFS traversal, you need to utilize a stack data structure with a maximum size equal to the total number of vertices in the graph.
To implement DFS traversal, you need to take the following stages.
Step 1: Create a stack with the total number of vertices in the graph as the size.
Step 2: Choose any vertex as the traversal's beginning point. Push a visit to that vertex and add it to the stack.
Step 3 - Push any non-visited adjacent vertices of a vertex at the top of the stack to the top of the stack.
Step 4 - Repeat steps 3 and 4 until there are no more vertices to visit from the vertex at the top of the stack.
Step 5 - If there are no new vertices to visit, go back and pop one from the stack using backtracking.
Step 6 - Continue using steps 3, 4, and 5 until the stack is empty.
Step 7 - When the stack is entirely unoccupied, create the final spanning tree by deleting the graph's unused edges.
Consider the following graph as an example of how to use the dfs algorithm.
 |
| Backtracking algorithm description |
Step 1: Mark vertex A as a visited source node by selecting it as a source node.
- You should push vertex A to the top of the stack.
 |
| Backtracking algorithm description |
Step 2: Any nearby unvisited vertex of vertex A, say B, should be visited.
- You should push vertex B to the top of the stack.
 |
| Backtracking algorithm description |
Step 3: From vertex C and D, visit any adjacent unvisited vertices of vertex B. Imagine you have chosen vertex C, and you want to make C a visited vertex.
- Vertex C is pushed to the top of the stack.
 |
| Backtracking algorithm description |
Step 4: You can visit any nearby unvisited vertices of vertex C, you need to select vertex D and designate it as a visited vertex.
- Vertex D is pushed to the top of the stack.
 |
| Backtracking algorithm description |
 |
| Backtracking algorithm description |
Step 5: Vertex E is the lone unvisited adjacent vertex of vertex D, thus marking it as visited.
- Vertex E should be pushed to the top of the stack.
 |
| Backtracking algorithm description |
Step 6: Vertex E's nearby vertices, namely vertex C and D have been visited, pop vertex E from the stack.
 |
| Backtracking algorithm description |
Step 7: Now that all of vertex D's nearby vertices, namely vertex B and C, have been visited, pop vertex D from the stack.
 |
| Backtracking algorithm description |
Step 8: Similarly, vertex C's adjacent vertices have already been visited; therefore, pop it from the stack.
 |
| Backtracking algorithm description |
Step 9: There is no more unvisited adjacent vertex of b, thus pop it from the stack.
 |
| Backtracking algorithm description |
Step 10: All of the nearby vertices of Vertex A, B, and C, have already been visited, so pop vertex A from the stack as well.
 |
| Backtracking algorithm description |
When a dead-end occurs in any iteration, the Depth First Search (DFS) method traverses a network in a deathward motion and uses a stack data structure to remember to acquire the next vertex to start a search.

No comments:
Post a Comment